Gear & Accessory Set for Baby Doll, Pink

Rotating circular car part with teeth that mesh with some other toothed part

Ii intermeshing gears transmitting rotational motion. Since the larger gear is rotating less quickly, its torque is proportionally greater. 1 subtlety of this detail arrangement is that the linear speed at the pitch bore is the same on both gears.

Multiple reducer gears in a microwave oven (measuring record shows scale)

A gear is a rotating circular motorcar role having cut teeth or, in the instance of a cogwheel or gearwheel, inserted teeth (called cogs), which mesh with another (uniform) toothed part to transmit (convert) torque and speed. The bones principle behind the operation of gears is coordinating to the basic principle of levers.^[i] A gear may besides exist known informally as a cog. Geared devices can modify the speed, torque, and direction of a power source. Gears of unlike sizes produce a change in torque, creating a mechanical advantage, through their gear ratio, and thus may exist considered a simple machine. The rotational speeds, and the torques, of 2 meshing gears differ in proportion to their diameters. The teeth on the two meshing gears all have the same shape.^[2]

Two or more than meshing gears, working in a sequence, are called a gear railroad train or a transmission. The gears in a manual are analogous to the wheels in a crossed, belt pulley arrangement. An advantage of gears is that the teeth of a gear preclude slippage. In transmissions with multiple gear ratios—such as bicycles, motorcycles, and cars—the term "gear" (e.g., "showtime gear") refers to a gear ratio rather than an bodily concrete gear. The term describes similar devices, even when the gear ratio is continuous rather than discrete, or when the device does not actually contain gears, every bit in a continuously variable transmission.^[three]

Furthermore, a gear can mesh with a linear toothed part, chosen a rack, producing translation instead of rotation.

History [edit]

Early examples of gears date from the 4th century BC in Communist china^[four] (Zhan Guo times – Late Eastward Zhou dynasty), which have been preserved at the Luoyang Museum of Henan Province, China. The earliest preserved gears in Europe were found in the Antikythera mechanism, an example of a very early on and intricate geared device, designed to calculate astronomical positions. Its time of construction is now estimated between 150 and 100 BC.^[5] Gears announced in works continued to Hero of Alexandria, in Roman Egypt circa Ad l,^[6] just tin exist traced back to the mechanics of the Alexandrian school in third-century BC Ptolemaic Arab republic of egypt, and were profoundly developed by the Greek polymath Archimedes (287–212 BC).^[7]

Single-stage gear reducer

The segmental gear, which receives/communicates reciprocating movement from/to a cogwheel, consisting of a sector of a round gear/ring having cogs on the periphery,^[8] was invented past Arab engineer Al-Jazari in 1206.^[ix] The worm gear was invented in the Indian subcontinent, for use in roller cotton wool gins, some fourth dimension during the 13th–14th centuries.^[10] Differential gears may take been used in some of the Chinese south-pointing chariots,^[11] but the showtime verifiable use of differential gears was by the British clock maker Joseph Williamson in 1720.

Examples of early on gear applications include:

1386 CE: The Salisbury Cathedral clock: it is the world'south oldest still working geared mechanical clock.
c. 13th–14th centuries: The worm gear was invented as function of a roller cotton gin in the Indian subcontinent.^[10]
c. 1221 CE The geared astrolabe was congenital in Isfahan showing the position of the moon in the zodiac and its phase, and the number of days since new moon.^[12]
c. 1206 CE:Al-Jazari invented the segmental gear every bit part of a h2o-lifting device.^[nine]
725 CE: The start geared mechanical clocks were built in China.
c. 200–265 CE: Ma Jun used gears as part of a south-pointing chariot.
2d century BC: The Antikythera machinery
In nature: in the hind legs of the nymphs of the planthopper insect Issus coleoptratus.

Etymology [edit]

The word gear is probably from Old Norse gørvi (plural gørvar) 'apparel, gear,' related to gøra, gørva 'to brand, construct, build; fix in order, prepare,' a mutual verb in Onetime Norse, "used in a wide range of situations from writing a book to dressing meat". In this context, the significant of 'toothed wheel in machinery' first attested 1520s; specific mechanical sense of 'parts by which a motor communicates motion' is from 1814; specifically of a vehicle (bicycle, automobile, etc.) by 1888.^[13]

Wooden cogwheel driving a lantern pinion or cage gear

A cast gearwheel (above) meshing with a cogged mortise bike (below). The wooden cogs are held in place past nails.

A cog is a tooth on a wheel. From Middle English cogge, from One-time Norse (compare Norwegian kugg ('cog'), Swedish kugg, kugge ('cog, molar')), from Proto-Germanic *kuggō (compare Dutch kogge ('cogboat'), German Kock), from Proto-Indo-European *gugā ('hump, ball') (compare Lithuanian gugà ('pommel, hump, hill'), from PIE *gēw- ('to bend, arch').^[14] First used c. 1300 in the sense of 'a wheel having teeth or cogs; tardily 14c., 'molar on a wheel'; cog-wheel, early 15c.^[15]

Historically, cogs were teeth made of woods rather than metallic, and a cogwheel technically consisted of a series of wooden gear teeth located around a mortise wheel, each tooth forming a blazon of specialised 'through' mortise and tenon joint. The wheel can be made of wood, cast iron, or other material. Wooden cogs were formerly used when big metal gears could not exist cut, when the cast molar was not even approximately of the proper shape, or the size of the wheel fabricated industry impractical.^[16]

The cogs were oft made of maple wood. In 1967 the Thompson Manufacturing Company of Lancaster, New Hampshire still had a very active business organization in supplying tens of thousands of maple gear teeth per twelvemonth, generally for use in paper mills and grist mills, some dating back over 100 years.^[17] Since a wooden cog performs exactly the same role as a bandage or machined metal tooth, the discussion was applied past extension to both, and the distinction has been by and large lost.

Comparison with bulldoze mechanisms [edit]

The definite ratio that teeth give gears provides an advantage over other drives (such as traction drives and V-belts) in precision machines such as watches that depend upon an exact velocity ratio. In cases where commuter and follower are proximal, gears also have an advantage over other drives in the reduced number of parts required. The downside is that gears are more expensive to manufacture and their lubrication requirements may impose a higher operating cost per hour.

Types [edit]

External versus internal gears [edit]

An external gear is one with the teeth formed on the outer surface of a cylinder or cone. Conversely, an internal gear is one with the teeth formed on the inner surface of a cylinder or cone. For bevel gears, an internal gear is one with the pitch bending exceeding 90 degrees. Internal gears do not crusade output shaft direction reversal.^[18]

Spur [edit]

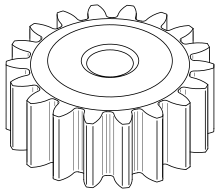
Spur gears or straight-cut gears are the simplest type of gear. They consist of a cylinder or disk with teeth projecting radially. Though the teeth are not straight-sided (but usually of special form to accomplish a constant drive ratio, mainly involute but less unremarkably cycloidal), the edge of each tooth is straight and aligned parallel to the axis of rotation. These gears mesh together correctly only if fitted to parallel shafts.^[19] No centric thrust is created by the molar loads. Spur gears are excellent at moderate speeds but tend to exist noisy at high speeds.^[20]

Helical [edit]

An external contact helical gear in activeness

Helical gears
Acme: parallel configuration
Bottom: crossed configuration

Helical or "dry fixed" gears offer a refinement over spur gears. The leading edges of the teeth are not parallel to the centrality of rotation, but are prepare at an angle. Since the gear is curved, this angling makes the tooth shape a segment of a helix. Helical gears tin exist meshed in parallel or crossed orientations. The former refers to when the shafts are parallel to each other; this is the most common orientation. In the latter, the shafts are non-parallel, and in this configuration the gears are sometimes known as "skew gears".

The angled teeth engage more gradually than practise spur gear teeth, causing them to run more than smoothly and quietly.^[21] With parallel helical gears, each pair of teeth first brand contact at a single point at one side of the gear cycle; a moving bend of contact then grows gradually across the tooth face to a maximum, then recedes until the teeth break contact at a single betoken on the opposite side. In spur gears, teeth of a sudden meet at a line contact across their entire width, causing stress and racket. Spur gears make a feature whine at high speeds. For this reason spur gears are used in depression-speed applications and in situations where noise control is non a problem, and helical gears are used in high-speed applications, large ability transmission, or where noise abatement is important.^[22] The speed is considered high when the pitch line velocity exceeds 25 yard/s.^[23]

A disadvantage of helical gears is a resultant thrust along the axis of the gear, which must be accommodated past advisable thrust bearings. However, this issue can be turned into an advantage when using a herringbone gear or double helical gear, which has no axial thrust - and besides provides cocky-aligning of the gears. This results in less axial thrust than a comparable spur gear.

A second disadvantage of helical gears is as well a greater degree of sliding friction betwixt the meshing teeth, often addressed with additives in the lubricant.

Skew gears [edit]

For a "crossed" or "skew" configuration, the gears must have the same pressure bending and normal pitch; however, the helix bending and handedness can exist different. The relationship betwixt the ii shafts is actually defined past the helix bending(south) of the two shafts and the handedness, as divers:^[24]

Due east=\beta _{one}+\beta _{2}

for gears of the aforementioned handedness,

E=\beta _{1}-\beta _{2}

for gears of reverse handedness,

where $\beta$ is the helix bending for the gear. The crossed configuration is less mechanically audio considering there is simply a point contact between the gears, whereas in the parallel configuration in that location is a line contact.^[24]

Quite normally, helical gears are used with the helix angle of ane having the negative of the helix angle of the other; such a pair might likewise be referred to every bit having a right-handed helix and a left-handed helix of equal angles. The two equal but contrary angles add to zero: the bending between shafts is zero—that is, the shafts are parallel. Where the sum or the deviation (equally described in the equations in a higher place) is not nix, the shafts are crossed. For shafts crossed at right angles, the helix angles are of the same mitt because they must add together to 90 degrees. (This is the case with the gears in the illustration in a higher place: they mesh correctly in the crossed configuration: for the parallel configuration, one of the helix angles should exist reversed. The gears illustrated cannot mesh with the shafts parallel.)

3D animation of helical gears (parallel centrality)
3D animation of helical gears (crossed axis)

Double helical [edit]

Double helical gears overcome the problem of axial thrust presented by unmarried helical gears past using a double ready of teeth, slanted in reverse directions. A double helical gear tin can be thought of equally two mirrored helical gears mounted closely together on a mutual axle. This arrangement cancels out the cyberspace axial thrust, since each half of the gear thrusts in the opposite direction, resulting in a net axial force of zero. This system can besides remove the need for thrust bearings. However, double helical gears are more than difficult to industry due to their more than complicated shape.

Herringbone gears are a special type of helical gears. They do not have a groove in the center like some other double helical gears practise; the two mirrored helical gears are joined together and then that their teeth form a Five shape. This can also be applied to bevel gears, as in the final drive of the Citroën Type A.

For both possible rotational directions, at that place exist two possible arrangements for the oppositely-oriented helical gears or gear faces. Ane arrangement is called stable, and the other unstable. In a stable arrangement, the helical gear faces are oriented so that each axial strength is directed toward the center of the gear. In an unstable arrangement, both axial forces are directed away from the center of the gear. In either arrangement, the total (or cyberspace) axial forcefulness on each gear is zip when the gears are aligned correctly. If the gears get misaligned in the axial direction, the unstable arrangement generates a net strength that may lead to disassembly of the gear train, while the stable organisation generates a net corrective strength. If the direction of rotation is reversed, the direction of the axial thrusts is besides reversed, so a stable configuration becomes unstable, and vice versa.

Stable double helical gears can be straight interchanged with spur gears without whatsoever need for dissimilar bearings.

Bevel [edit]

Wooden cogs set in bevel mortise wheels driving a millstone. Note wooden spur gears in the background.

A bevel gear is shaped like a right round cone with most of its tip cutting off. When two bevel gears mesh, their imaginary vertices must occupy the same point. Their shaft axes also intersect at this point, forming an arbitrary not-straight angle between the shafts. The angle between the shafts can be annihilation except aught or 180 degrees. Bevel gears with equal numbers of teeth and shaft axes at xc degrees are called miter (United states) or mitre (UK) gears.

Screw bevels [edit]

Screw bevel gears can be manufactured as Gleason types (circular arc with not-constant tooth depth), Oerlikon and Curvex types (circular arc with abiding tooth depth), Klingelnberg Cyclo-Palloid (Epicycloid with abiding tooth depth) or Klingelnberg Palloid. Screw bevel gears accept the aforementioned advantages and disadvantages relative to their straight-cutting cousins as helical gears practice to spur gears. Directly bevel gears are generally used only at speeds below 5 m/s (1000 ft/min), or, for small gears, grand r.p.m.^[25]

Notation: The cylindrical gear tooth profile corresponds to an anfractuous, but the bevel gear molar profile to an octoid. All traditional bevel gear generators (similar Gleason, Klingelnberg, Heidenreich & Harbeck, WMW Modul) manufacture bevel gears with an octoidal tooth profile. IMPORTANT: For 5-centrality milled bevel gear sets it is of import to choose the same calculation / layout like the conventional manufacturing method. Simplified calculated bevel gears on the basis of an equivalent cylindrical gear in normal section with an involute tooth form show a deviant tooth form with reduced tooth strength by 10-28% without offset and 45% with commencement [Diss. Hünecke, TU Dresden]. Furthermore, the "anfractuous bevel gear sets" cause more racket.

Hypoid [edit]

Hypoid gears resemble spiral bevel gears except the shaft axes do not intersect. The pitch surfaces appear conical but, to compensate for the offset shaft, are in fact hyperboloids of revolution.^[26] ^[27] Hypoid gears are nearly ever designed to operate with shafts at 90 degrees. Depending on which side the shaft is offset to, relative to the angling of the teeth, contact between hypoid gear teeth may be even smoother and more gradual than with spiral bevel gear teeth, only likewise take a sliding activity forth the meshing teeth equally it rotates and therefore usually crave some of the most gluey types of gear oil to avert it beingness extruded from the mating tooth faces, the oil is normally designated HP (for hypoid) followed past a number denoting the viscosity. Likewise, the pinion tin can be designed with fewer teeth than a spiral bevel pinion, with the result that gear ratios of 60:1 and higher are viable using a single ready of hypoid gears.^[28] This style of gear is most common in motor vehicle bulldoze trains, in concert with a differential. Whereas a regular (nonhypoid) ring-and-pinion gear ready is suitable for many applications, it is not ideal for vehicle bulldoze trains because it generates more noise and vibration than a hypoid does. Bringing hypoid gears to market for mass-production applications was an engineering improvement of the 1920s.

Crown [edit]

Crown gears or contrate gears are a particular form of bevel gear whose teeth project at right angles to the plane of the wheel; in their orientation the teeth resemble the points on a crown. A crown gear can just mesh accurately with another bevel gear, although crown gears are sometimes seen meshing with spur gears. A crown gear is also sometimes meshed with an escapement such as constitute in mechanical clocks.

Worm [edit]

Worms resemble screws. A worm is meshed with a worm bike, which looks similar to a spur gear.

Worm-and-gear sets are a simple and meaty mode to achieve a high torque, low speed gear ratio. For case, helical gears are normally limited to gear ratios of less than ten:1 while worm-and-gear sets vary from 10:i to 500:1.^[29] A disadvantage is the potential for considerable sliding action, leading to low efficiency.^[thirty]

A worm gear is a species of helical gear, merely its helix angle is ordinarily somewhat large (close to 90 degrees) and its body is commonly adequately long in the axial management. These attributes give information technology screw similar qualities. The distinction between a worm and a helical gear is that at to the lowest degree one molar persists for a full rotation around the helix. If this occurs, it is a 'worm'; if not, it is a 'helical gear'. A worm may accept as few as i tooth. If that molar persists for several turns around the helix, the worm appears, superficially, to accept more than than i molar, only what one in fact sees is the same tooth reappearing at intervals forth the length of the worm. The usual spiral classification applies: a one-toothed worm is chosen single thread or single beginning; a worm with more than 1 molar is called multiple thread or multiple start. The helix bending of a worm is non usually specified. Instead, the lead angle, which is equal to 90 degrees minus the helix angle, is given.

In a worm-and-gear fix, the worm can always drive the gear. Withal, if the gear attempts to drive the worm, it may or may not succeed. Specially if the lead angle is small, the gear's teeth may simply lock against the worm's teeth, because the strength component circumferential to the worm is not sufficient to overcome friction. In traditional music boxes, notwithstanding, the gear drives the worm, which has a large helix angle. This mesh drives the speed-limiter vanes which are mounted on the worm shaft.

Worm-and-gear sets that practice lock are called cocky locking, which can be used to advantage, equally when it is desired to fix the position of a machinery by turning the worm and then have the mechanism concord that position. An example is the machine head establish on some types of stringed instruments.

If the gear in a worm-and-gear set is an ordinary helical gear just a single point of contact is achieved.^[28] ^[31] If medium to loftier power transmission is desired, the tooth shape of the gear is modified to achieve more intimate contact by making both gears partially envelop each other. This is done by making both concave and joining them at a saddle indicate; this is called a cone-drive ^[32] or "Double enveloping".

Worm gears can be right or left-handed, following the long-established practice for screw threads.^[18]

3D Blitheness of a worm-gear set

Non-circular [edit]

Non-circular gears are designed for special purposes. While a regular gear is optimized to transmit torque to some other engaged fellow member with minimum dissonance and wear and maximum efficiency, a not-circular gear'southward chief objective might be ratio variations, beam displacement oscillations and more. Common applications include fabric machines, potentiometers and continuously variable transmissions.

Rack and pinion [edit]

Rack and pinion gearing

A rack is a toothed bar or rod that tin can be thought of as a sector gear with an infinitely big radius of curvature. Torque can be converted to linear force past meshing a rack with a round gear called a pinion: the pinion turns, while the rack moves in a direct line. Such a mechanism is used in automobiles to convert the rotation of the steering wheel into the left-to-correct motion of the tie rod(s).

Racks too feature in the theory of gear geometry, where, for instance, the tooth shape of an interchangeable fix of gears may exist specified for the rack (infinite radius), and the molar shapes for gears of particular actual radii are then derived from that. The rack and pinion gear blazon is also used in a rack railway.

Epicyclic [edit]

In epicyclic gearing, one or more of the gear axes moves. Examples are lord's day and planet gearing (come across below), cycloidal drive, automatic transmissions, and mechanical differentials.

Sunday and planet [edit]

Sun (yellowish) and planet (ruby) gearing

Sun and planet gearing is a method of converting reciprocating motion into rotary motion that was used in steam engines. James Watt used it on his early steam engines to get around the patent on the crank, just information technology also provided the advantage of increasing the flywheel speed and so Watt could utilize a lighter flywheel.

In the illustration, the dominicus is yellow, the planet red, the reciprocating arm is blue, the flywheel is dark-green and the driveshaft is gray.

Harmonic gear [edit]

A harmonic gear or strain moving ridge gear is a specialized gearing machinery frequently used in industrial motion control, robotics and aerospace for its advantages over traditional gearing systems, including lack of backlash, compactness and loftier gear ratios.

Though the diagram does not demonstrate the correct configuration, it is a "timing gear," conventionally with far more teeth than a traditional gear to ensure a higher caste of precision.

Cage gear [edit]

Cage gear in Pantigo Windmill, Long Island (with the driving gearwheel disengaged)

A cage gear, also chosen a lantern gear or lantern pinion, has cylindrical rods for teeth, parallel to the axle and arranged in a circle around information technology, much as the bars on a round bird muzzle or lantern. The assembly is held together by disks at each end, into which the tooth rods and axle are set. Cage gears are more efficient than solid pinions,^{[ citation needed ]} and dirt tin fall through the rods rather than becoming trapped and increasing wear. They can be constructed with very unproblematic tools as the teeth are non formed by cutting or milling, but rather by drilling holes and inserting rods.

Sometimes used in clocks, the muzzle gear should always be driven by a gearwheel, not used as the driver. The cage gear was not initially favoured by bourgeois clock makers. It became popular in turret clocks where dirty working conditions were most commonplace. Domestic American clock movements oftentimes used them.

Cycloidal gear [edit]

Magnetic gear [edit]

All cogs of each gear component of magnetic gears act every bit a constant magnet with periodic alternation of opposite magnetic poles on mating surfaces. Gear components are mounted with a backfire capability similar to other mechanical gearings. Although they cannot exert as much forcefulness as a traditional gear due to limits on magnetic field strength, such gears piece of work without touching and so are immune to wear, take very low dissonance, no power losses from friction and tin slip without impairment making them very reliable.^[33] They tin be used in configurations that are not possible for gears that must be physically touching and can operate with a non-metallic barrier completely separating the driving forcefulness from the load. The magnetic coupling can transmit forcefulness into a hermetically sealed enclosure without using a radial shaft seal, which may leak.

Nomenclature [edit]

General [edit]

Rotational frequency, n

Measured in rotation over time, such equally revolutions per minute (RPM or rpm).

Angular frequency, ω

Measured in radians/second. 1RPM = 2πrad/minute = π/30rad/second.

Number of teeth, North

How many teeth a gear has, an integer. In the case of worms, information technology is the number of thread starts that the worm has.

Gear, wheel

The larger of two interacting gears or a gear on its own.

Pinion

The smaller of two interacting gears.

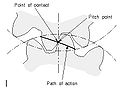
Path of contact

Path followed by the point of contact between two meshing gear teeth.

Line of action, pressure line

Line along which the force between two meshing gear teeth is directed. It has the same direction equally the force vector. In general, the line of action changes from moment to moment during the flow of engagement of a pair of teeth. For involute gears, withal, the tooth-to-tooth force is always directed forth the same line—that is, the line of action is constant. This implies that for involute gears the path of contact is also a directly line, coincident with the line of action—equally is indeed the case.

Axis

Centrality of revolution of the gear; eye line of the shaft.

Pitch betoken

Point where the line of activity crosses a line joining the 2 gear axes.

Pitch circle, pitch line

Circle centered on and perpendicular to the centrality, and passing through the pitch point. A predefined diametral position on the gear where the circular tooth thickness, pressure level angle and helix angles are defined.

Pitch diameter, d

A predefined diametral position on the gear where the round tooth thickness, pressure level angle and helix angles are defined. The standard pitch diameter is a design dimension and cannot be measured, but is a location where other measurements are made. Its value is based on the number of teeth (N), the normal module (m_n ; or normal diametral pitch, P_d ), and the helix angle (

\psi

d={\frac {Nm_{n}}{\cos \psi }}

in metric units or

d={\frac {Due north}{P_{d}\cos \psi }}

in royal units.^[34]

Module or modulus, m

Since information technology is impractical to calculate circular pitch with irrational numbers, mechanical engineers normally apply a scaling factor that replaces it with a regular value instead. This is known every bit the module or modulus of the wheel and is simply defined every bit:

m={\frac {p}{\pi }}

where m is the module and p the circular pitch. The units of module are customarily millimeters; an English Module is sometimes used with the units of inches. When the diametral pitch, DP, is in English language units,

m={\frac {25.4}{DP}}

in conventional metric units.

The distance between the two axis becomes:

a={\frac {grand}{ii}}(z_{1}+z_{2})

where a is the axis distance, z_i and z₂ are the number of cogs (teeth) for each of the 2 wheels (gears). These numbers (or at least one of them) is often called amidst primes to create an fifty-fifty contact between every cog of both wheels, and thereby avoid unnecessary wear and damage. An even uniform gear article of clothing is achieved by ensuring the tooth counts of the ii gears meshing together are relatively prime number to each other; this occurs when the greatest common divisor (GCD) of each gear tooth count equals ane, e.m. GCD(16,25)=1; if a i:1 gear ratio is desired a relatively prime gear may be inserted in between the two gears; this maintains the 1:1 ratio but reverses the gear direction; a second relatively prime gear could also be inserted to restore the original rotational direction while maintaining uniform wear with all 4 gears in this instance. Mechanical engineers, at least in continental Europe, usually employ the module instead of circular pitch. The module, only like the circular pitch, can be used for all types of cogs, not merely evolvent based directly cogs.^[35]

Operating pitch diameters

Diameters determined from the number of teeth and the center altitude at which gears operate.^[xviii] Example for pinion:

d_{w}={\frac {2a}{u+1}}={\frac {2a}{{\frac {z_{2}}{z_{one}}}+one}}.

Pitch surface

In cylindrical gears, cylinder formed past projecting a pitch circle in the centric management. More generally, the surface formed by the sum of all the pitch circles every bit one moves along the axis. For bevel gears it is a cone.

Bending of action

Angle with vertex at the gear center, one leg on the point where mating teeth first make contact, the other leg on the point where they disengage.

Arc of action

Segment of a pitch circle subtended past the angle of action.

Pressure bending, $\theta$

The complement of the angle between the management that the teeth exert forcefulness on each other, and the line joining the centers of the two gears. For involute gears, the teeth always exert force along the line of activeness, which, for involute gears, is a straight line; and thus, for involute gears, the pressure angle is abiding.

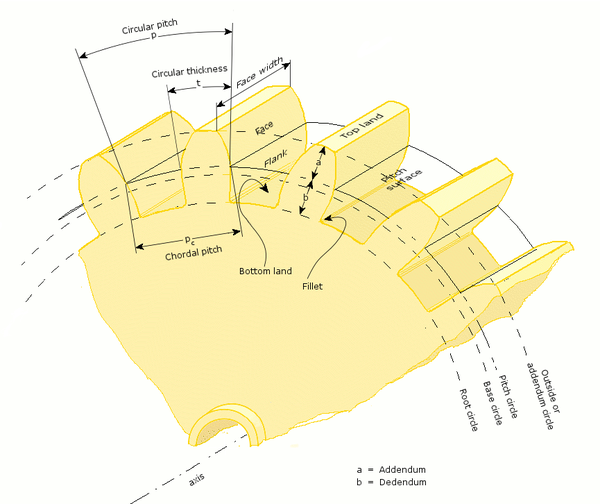
Outside diameter, $D_{o}$

Diameter of the gear, measured from the tops of the teeth.

Root bore

Bore of the gear, measured at the base of the tooth.

Annex, a

Radial distance from the pitch surface to the outermost point of the tooth.

a={\frac {1}{two}}(D_{o}-D)

Dedendum, b

Radial distance from the depth of the tooth trough to the pitch surface.

b={\frac {ane}{2}}(D-{\text{root diameter}})

Whole depth, $h_{t}$

The distance from the superlative of the tooth to the root; it is equal to addendum plus dedendum or to working depth plus clearance.

Clearance

Distance between the root circumvolve of a gear and the addendum circle of its mate.

Working depth

Depth of date of 2 gears, that is, the sum of their operating addendums.

Circular pitch, p

Distance from ane confront of a tooth to the corresponding face of an side by side tooth on the aforementioned gear, measured along the pitch circle.

Diametral pitch, DP

DP={\frac {N}{d}}={\frac {\pi }{p}}

Ratio of the number of teeth to the pitch bore. Could be measured in teeth per inch or teeth per centimeter, but conventionally has units of per inch of bore. Where the module, one thousand, is in metric units

DP={\frac {25.4}{m}}

in English units

Base of operations circumvolve: In involute gears, the molar profile is generated past the involute of the base circle. The radius of the base of operations circumvolve is somewhat smaller than that of the pitch circle
Base pitch, normal pitch, $p_{b}$: In involute gears, distance from one face of a tooth to the corresponding face of an next tooth on the aforementioned gear, measured along the base of operations circle
Interference: Contact between teeth other than at the intended parts of their surfaces
Interchangeable prepare: A set of gears, any of which mates properly with any other

Helical gear [edit]

Helix angle, $\psi$: the Angle between a tangent to the helix and the gear axis. Information technology is aught in the limiting instance of a spur gear, admitting it tin can considered as the hypotenuse angle also.
Normal circular pitch, $p_{n}$: Circular pitch in the plane normal to the teeth.
Transverse round pitch, p: Round pitch in the plane of rotation of the gear. Sometimes just chosen "circular pitch". $p_{due north}=p\cos(\psi )$

Several other helix parameters tin can be viewed either in the normal or transverse planes. The subscript n ordinarily indicates the normal.

Worm gear [edit]

Atomic number 82: Distance from any point on a thread to the respective point on the next turn of the aforementioned thread, measured parallel to the axis.
Linear pitch, p: Altitude from whatever point on a thread to the corresponding indicate on the adjacent thread, measured parallel to the axis. For a single-thread worm, lead and linear pitch are the same.
Lead angle, $\lambda$: Bending between a tangent to the helix and a aeroplane perpendicular to the axis. Note that the complement of the helix angle is unremarkably given for helical gears.
Pitch bore, $d_{westward}$: Same as described earlier in this listing. Note that for a worm information technology is still measured in a plane perpendicular to the gear axis, not a tilted plane.

Subscript w denotes the worm, subscript g denotes the gear.

Tooth contact [edit]

Line of contact
Path of action
Line of action
Plane of action
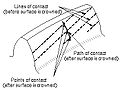
Lines of contact (helical gear)
Arc of activity
Length of action
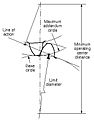
Limit diameter
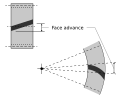
Face advance
Zone of action

Point of contact

Whatsoever betoken at which two molar profiles impact each other.

Line of contact

A line or curve along which two tooth surfaces are tangent to each other.

Path of action

The locus of successive contact points between a pair of gear teeth, during the phase of engagement. For cohabit gear teeth, the path of activeness passes through the pitch point. Information technology is the trace of the surface of action in the airplane of rotation.

Line of activeness

The path of action for involute gears. It is the straight line passing through the pitch signal and tangent to both base of operations circles.

Surface of action

The imaginary surface in which contact occurs between two engaging tooth surfaces. It is the summation of the paths of action in all sections of the engaging teeth.

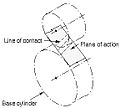
Aeroplane of action

The surface of action for involute, parallel centrality gears with either spur or helical teeth. Information technology is tangent to the base cylinders.

Zone of activity (contact zone)

For involute, parallel-centrality gears with either spur or helical teeth, is the rectangular area in the aeroplane of activity bounded by the length of activeness and the effective confront width.

Path of contact

The bend on either tooth surface along which theoretical unmarried indicate contact occurs during the engagement of gears with crowned tooth surfaces or gears that normally engage with simply unmarried point contact.

Length of action

The distance on the line of action through which the point of contact moves during the action of the tooth profile.

Arc of activeness, Q_t

The arc of the pitch circle through which a tooth profile moves from the kickoff to the end of contact with a mating profile.

Arc of approach, Q_a

The arc of the pitch circle through which a tooth profile moves from its beginning of contact until the point of contact arrives at the pitch point.

Arc of recess, Q_r

The arc of the pitch circle through which a tooth profile moves from contact at the pitch point until contact ends.

Contact ratio, m_c, ε

The number of angular pitches through which a tooth surface rotates from the beginning to the end of contact. In a simple style, it can be defined as a measure out of the average number of teeth in contact during the period during which a tooth comes and goes out of contact with the mating gear.

Transverse contact ratio, m_p, ε_α

The contact ratio in a transverse plane. It is the ratio of the angle of activity to the angular pitch. For involute gears it is near straight obtained equally the ratio of the length of activity to the base pitch.

Face contact ratio, m_F, ε_β

The contact ratio in an centric plane, or the ratio of the face up width to the axial pitch. For bevel and hypoid gears information technology is the ratio of face advance to circular pitch.

Full contact ratio, one thousand_t, ε_γ

The sum of the transverse contact ratio and the face up contact ratio.

\epsilon _{\gamma }=\epsilon _{\alpha }+\epsilon _{\beta }

m_{\rm {t}}=m_{\rm {p}}+m_{\rm {F}}

Modified contact ratio, g_o

For bevel gears, the square root of the sum of the squares of the transverse and face contact ratios.

m_{\rm {o}}={\sqrt {m_{\rm {p}}^{ii}+m_{\rm {F}}^{two}}}

Limit bore: Diameter on a gear at which the line of activity intersects the maximum (or minimum for internal pinion) annex circle of the mating gear. This is also referred to as the starting time of agile profile, the commencement of contact, the end of contact, or the end of agile contour.
Start of active profile (SAP): Intersection of the limit diameter and the anfractuous profile.
Face advance: Distance on a pitch circle through which a helical or spiral molar moves from the position at which contact begins at one end of the molar trace on the pitch surface to the position where contact ceases at the other end.

Tooth thickness [edit]

Molar thickness
Thickness relationships
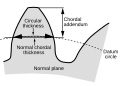
Chordal thickness
Tooth thickness measurement over pins
Span measurement
Long and curt addendum teeth

Round thickness: Length of arc between the 2 sides of a gear tooth, on the specified datum circle.
Transverse circular thickness: Round thickness in the transverse plane.
Normal round thickness: Circular thickness in the normal plane. In a helical gear it may be considered as the length of arc along a normal helix.
Axial thickness: In helical gears and worms, tooth thickness in an centric cross section at the standard pitch bore.
Base circular thickness: In involute teeth, length of arc on the base circle between the two involute curves forming the contour of a molar.
Normal chordal thickness: Length of the chord that subtends a circular thickness arc in the plane normal to the pitch helix. Whatever convenient measuring diameter may be selected, not necessarily the standard pitch bore.
Chordal addendum (chordal height): Height from the pinnacle of the tooth to the chord subtending the circular thickness arc. Any user-friendly measuring diameter may be selected, not necessarily the standard pitch diameter.
Profile shift: Deportation of the basic rack datum line from the reference cylinder, made not-dimensional by dividing by the normal module. Information technology is used to specify the tooth thickness, often for zero backlash.
Rack shift: Displacement of the tool datum line from the reference cylinder, made non-dimensional by dividing by the normal module. It is used to specify the molar thickness.
Measurement over pins: Measurement of the altitude taken over a pin positioned in a molar infinite and a reference surface. The reference surface may be the reference centrality of the gear, a datum surface or either ane or two pins positioned in the tooth space or spaces opposite the showtime. This measurement is used to determine molar thickness.
Bridge measurement: Measurement of the distance across several teeth in a normal plane. Equally long equally the measuring device has parallel measuring surfaces that contact on an unmodified portion of the anfractuous, the measurement wis along a line tangent to the base cylinder. Information technology is used to decide tooth thickness.
Modified addendum teeth: Teeth of engaging gears, one or both of which accept non-standard annex.
Full-depth teeth: Teeth in which the working depth equals two.000 divided past the normal diametral pitch.
Stub teeth: Teeth in which the working depth is less than 2.000 divided by the normal diametral pitch.
Equal addendum teeth: Teeth in which two engaging gears take equal addendums.
Long and short-annex teeth: Teeth in which the addendums of two engaging gears are unequal.

Pitch [edit]

Pitch is the distance between a indicate on one tooth and the corresponding betoken on an adjacent tooth.^[18] It is a dimension measured along a line or bend in the transverse, normal, or axial directions. The apply of the unmarried word pitch without qualification may be cryptic, and for this reason it is preferable to use specific designations such as transverse circular pitch, normal base pitch, axial pitch.

Pitch
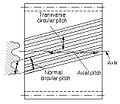
Tooth pitch
Base of operations pitch relationships
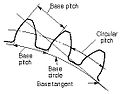
Primary pitches

Circular pitch, p

Arc distance forth a specified pitch circle or pitch line between corresponding profiles of adjacent teeth.

Transverse circular pitch, p _t

Round pitch in the transverse aeroplane.

Normal circular pitch, p _{due north}, p _east

Circular pitch in the normal airplane, and also the length of the arc forth the normal pitch helix betwixt helical teeth or threads.

Centric pitch, p _x

Linear pitch in an axial airplane and in a pitch surface. In helical gears and worms, axial pitch has the same value at all diameters. In gearing of other types, axial pitch may exist bars to the pitch surface and may be a circular measurement. The term axial pitch is preferred to the term linear pitch. The axial pitch of a helical worm and the circular pitch of its worm gear are the same.

Normal base pitch, p _{Due north}, p _bn

An involute helical gear is the base pitch in the normal aeroplane. It is the normal distance between parallel helical anfractuous surfaces on the plane of action in the normal plane, or is the length of arc on the normal base helix. Information technology is a constant altitude in whatever helical involute gear.

Transverse base of operations pitch, p _b, p _bt

In an involute gear, the pitch is on the base circumvolve or forth the line of action. Corresponding sides of involute gear teeth are parallel curves, and the base pitch is the constant and fundamental distance between them forth a common normal in a transverse plane.

Diametral pitch (transverse), P _d

Ratio of the number of teeth to the standard pitch diameter in inches.

P_{\rm {d}}={\frac {N}{d}}={\frac {25.4}{yard}}={\frac {\pi }{p}}

Normal diametrical pitch, P _nd

Value of diametrical pitch in a normal plane of a helical gear or worm.

P_{\rm {nd}}={\frac {P_{\rm {d}}}{\cos \psi }}

Angular pitch, θ_N, τ

Angle subtended by the round pitch, ordinarily expressed in radians.

\tau ={\frac {360}{z}}

degrees or

{\frac {ii\pi }{z}}

radians

Backlash [edit]

Backlash is the mistake in motion that occurs when gears change management. It exists considering in that location is ever some gap between the trailing face of the driving tooth and the leading face of the tooth behind it on the driven gear, and that gap must be closed before force tin be transferred in the new direction. The term "backlash" tin can also be used to refer to the size of the gap, non merely the phenomenon information technology causes; thus, one could speak of a pair of gears as having, for example, "0.one mm of backfire." A pair of gears could be designed to have zero backlash, just this would presuppose perfection in manufacturing, uniform thermal expansion characteristics throughout the organisation, and no lubricant. Therefore, gear pairs are designed to take some backlash. It is unremarkably provided by reducing the tooth thickness of each gear past half the desired gap altitude. In the example of a big gear and a modest pinion, nevertheless, the backlash is usually taken entirely off the gear and the pinion is given full sized teeth. Backfire can also be provided by moving the gears further apart. The backlash of a gear train equals the sum of the backlash of each pair of gears, so in long trains backlash tin can go a problem.

For situations that require precision, such as instrumentation and command, backlash can be minimized through one of several techniques. For example, the gear can be separate along a airplane perpendicular to the centrality, 1 half fixed to the shaft in the usual manner, the other half placed alongside it, free to rotate most the shaft, only with springs between the two-halves providing relative torque betwixt them, so that one achieves, in effect, a single gear with expanding teeth. Another method involves tapering the teeth in the centric direction and letting the gear slide in the axial direction to take up slack.

Shifting of gears [edit]

In some machines (east.g., automobiles) it is necessary to alter the gear ratio to conform the task, a procedure known as gear shifting or changing gear. At that place are several means of shifting gears, for example:

Manual transmission
Automatic transmission
Derailleur gears, which are really sprockets in combination with a roller chain
Hub gears (also called epicyclic gearing or sun-and-planet gears)

There are several outcomes of gear shifting in motor vehicles. In the case of vehicle racket emissions, at that place are higher sound levels emitted when the vehicle is engaged in lower gears. The design life of the lower ratio gears is shorter, so cheaper gears may be used, which tend to generate more noise due to smaller overlap ratio and a lower mesh stiffness etc. than the helical gears used for the high ratios. This fact has been used to clarify vehicle-generated sound since the late 1960s, and has been incorporated into the simulation of urban roadway noise and respective design of urban racket barriers along roadways.^[36]

Tooth profile [edit]

Contour of a spur gear
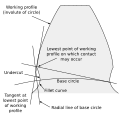
Undercut

A profile is one side of a tooth in a cross section between the outside circle and the root circle. Unremarkably a contour is the bend of intersection of a molar surface and a plane or surface normal to the pitch surface, such as the transverse, normal, or axial aeroplane.

The fillet curve (root fillet) is the concave portion of the tooth profile where it joins the lesser of the tooth space.²

As mentioned nearly the showtime of the article, the attainment of a nonfluctuating velocity ratio is dependent on the profile of the teeth. Friction and vesture between 2 gears is also dependent on the tooth profile. There are a peachy many molar profiles that provide constant velocity ratios. In many cases, given an capricious tooth shape, it is possible to develop a molar profile for the mating gear that provides a constant velocity ratio. Still, two constant velocity tooth profiles are the most ordinarily used in modern times: the cycloid and the involute. The cycloid was more than common until the tardily 1800s. Since so, the anfractuous has largely superseded it, particularly in bulldoze train applications. The cycloid is in some ways the more interesting and flexible shape; yet the anfractuous has two advantages: information technology is easier to manufacture, and it permits the middle-to-heart spacing of the gears to vary over some range without ruining the constancy of the velocity ratio. Cycloidal gears just work properly if the centre spacing is exactly right. Cycloidal gears are nevertheless used in mechanical clocks.

An undercut is a condition in generated gear teeth when any part of the fillet curve lies within of a line fatigued tangent to the working profile at its point of juncture with the fillet. Undercut may be deliberately introduced to facilitate finishing operations. With undercut the fillet bend intersects the working profile. Without undercut the fillet bend and the working contour take a mutual tangent.

Gear materials [edit]

Numerous nonferrous alloys, bandage irons, powder-metallurgy and plastics are used in the manufacture of gears. Even so, steels are most commonly used considering of their high forcefulness-to-weight ratio and depression price. Plastic is commonly used where cost or weight is a business. A properly designed plastic gear can supervene upon steel in many cases considering information technology has many desirable properties, including clay tolerance, low speed meshing, the ability to "skip" quite well^[37] and the power to be made with materials that don't need additional lubrication. Manufacturers have used plastic gears to reduce costs in consumer items including copy machines, optical storage devices, cheap dynamos, consumer audio equipment, servo motors, and printers. Another advantage of the use of plastics, formerly (such every bit in the 1980s), was the reduction of repair costs for certain expensive machines. In cases of severe jamming (as of the paper in a printer), the plastic gear teeth would exist torn costless of their substrate, allowing the drive mechanism to then spin freely (instead of damaging itself by straining against the jam). This use of "sacrificial" gear teeth avoided destroying the much more than expensive motor and related parts. This method has been superseded, in more recent designs, past the utilize of clutches and torque- or current-limited motors.

Standard pitches and the module arrangement [edit]

Although gears can be made with whatsoever pitch, for convenience and interchangeability standard pitches are frequently used. Pitch is a property associated with linear dimensions and so differs whether the standard values are in the royal (inch) or metric systems. Using inch measurements, standard diametral pitch values with units of "per inch" are chosen; the diametrical pitch is the number of teeth on a gear of one inch pitch bore. Common standard values for spur gears are iii, 4, 5, six, viii, 10, 12, sixteen, 20, 24, 32, 48, 64, 72, 80, 96, 100, 120, and 200.^[38] Sure standard pitches such as i/10 and 1/twenty in inch measurements, which mesh with linear rack, are actually (linear) circular pitch values with units of "inches"^[38]

When gear dimensions are in the metric system the pitch specification is by and large in terms of module or modulus, which is effectively a length measurement beyond the pitch bore. The term module is understood to hateful the pitch bore in millimetres divided by the number of teeth. When the module is based upon inch measurements, it is known equally the English language module to avoid confusion with the metric module. Module is a direct dimension, unlike diametrical pitch, which is an inverse dimension ("threads per inch"). Thus, if the pitch diameter of a gear is 40 mm and the number of teeth 20, the module is 2, which means that there are 2 mm of pitch diameter for each tooth.^[39] The preferred standard module values are 0.i, 0.two, 0.3, 0.iv, 0.5, 0.6, 0.viii, one.0, one.25, 1.5, 2.0, 2.v, 3, four, v, 6, 8, 10, 12, 16, 20, 25, 32, twoscore and 50.^[40]

Manufacture [edit]

As of 2014, an estimated 80% of all gearing produced worldwide is produced by internet shape molding. Molded gearing is usually either powder metallurgy or plastic.^[41] Many gears are done when they leave the mold (including injection molded plastic and dice cast metallic gears), but powdered metal gears require sintering and sand castings or investment castings require gear cut or other machining to finish them. The near mutual form of gear cutting is hobbing, merely gear shaping, milling, and broaching besides be. 3D printing as a product method is expanding rapidly. For metal gears in the transmissions of cars and trucks, the teeth are heat treated to make them hard and more wear resistant while leaving the core soft and tough. For large gears that are prone to warp, a quench press is used.

Gear model in modern physics [edit]

Modern physics adopted the gear model in different ways. In the nineteenth century, James Clerk Maxwell adult a model of electromagnetism in which magnetic field lines were rotating tubes of incompressible fluid. Maxwell used a gear wheel and called it an "idle wheel" to explain the electric electric current as a rotation of particles in reverse directions to that of the rotating field lines.^[42]

More recently, breakthrough physics uses "breakthrough gears" in their model. A grouping of gears tin serve every bit a model for several different systems, such as an artificially synthetic nanomechanical device or a group of ring molecules.^[43]

The three wave hypothesis compares the wave–particle duality to a bevel gear.^[44]

Gear mechanism in natural world [edit]

The gear mechanism was previously considered exclusively artificial, just every bit early on every bit 1957, gears had been recognized in the hind legs of various species of planthoppers^[45] and scientists from the University of Cambridge characterized their functional significance in 2013 by doing high-speed photography of the nymphs of Issus coleoptratus at Cambridge Academy.^[46] ^[47] These gears are plant simply in the nymph forms of all planthoppers, and are lost during the final molt to the adult stage.^[48] In I. coleoptratus, each leg has a 400-micrometer strip of teeth, pitch radius 200 micrometers, with 10 to 12 fully interlocking spur-type gear teeth, including filleted curves at the base of each tooth to reduce the take chances of shearing.^[49] The joint rotates like mechanical gears, and synchronizes Issus's hind legs when information technology jumps to within 30 microseconds, preventing yaw rotation.^[50] ^[51] ^[46] The gears are non connected all the time. 1 is located on each of the juvenile insect'southward hind legs, and when it prepares to jump, the two sets of teeth lock together. Every bit a result, the legs move in almost perfect unison, giving the insect more than power equally the gears rotate to their stopping indicate then unlock.^[50]

References [edit]

^ https://www.bbc.co.uk/bitesize/guides/ztjpb82/revision/3
^ "Definition of GEAR". merriam-webster.com . Retrieved 20 September 2018.
^ "Manual Basics". HowStuffWorks. 27 April 2005.
^ Derek J. de Solla Cost, On the Origin of Clockwork, Perpetual Move Devices, and the Compass, p.84
^ "The Antikythera Mechanism Inquiry Projection: Why is it and so of import?". Archived from the original on 4 May 2012. Retrieved 10 January 2011. The Mechanism is thought to date from betwixt 150 and 100 BC
^ Norton 2004, p. 462
^ Lewis, M. J. T. (1993). "Gearing in the Ancient Earth". Attempt. 17 (3): 110–115. doi:10.1016/0160-9327(93)90099-O.
^ "Segment gear". thefreedictionary.com . Retrieved 20 September 2018.
^ ^a ^b Donald Colina (2012), The Volume of Knowledge of Ingenious Mechanical Devices, page 273, Springer Science + Business organisation Media
^ ^a ^b Irfan Habib, Economical History of Medieval India, 1200-1500, page 53, Pearson Didactics
^ Joseph Needham (1986). Scientific discipline and Civilization in Prc: Volume 4, Part 2, page 298. Taipei: Caves Books, Ltd.
^ "Astrolabe Past Muhammad Ibn Abi Bakr Al Isfahani".
^ "gear (n.)". Etymonline . Retrieved thirteen February 2020.
^ "Etymology i: Cog (noun)". Wiktionary . Retrieved 29 July 2019.
^ "cog (n.)". Etymonline . Retrieved 13 February 2020.
^ Grant, George B. (1893). A Treatise on Gear Wheels (6th, illus. ed.). Lexington, MA; Philadelphia, PA: George B. Grant. p. 21.
^ Radzevich, Stephen P. (2012). Dudley'southward Handbook of Practical Gear Design and Industry (PDF) (2nd ed.). Boca Raton, FL.: CRC Press, an imprint of Taylor & Francis Grouping. pp. 691, 702.
^ ^a ^b ^c ^d American Gear Manufacturers Association; American National Standards Found, Gear Classification, Definitions of Terms with Symbols (ANSI/AGMA 1012-G05 ed.), American Gear Manufacturers Association
^ "How Gears Work". howstuffworks.com. sixteen November 2000. Retrieved xx September 2018.
^ Machinery'southward Handbook . New York: Industrial Press. 2012. pp. 2125. ISBN978-0-8311-2900-2.
^ Khurmi, R. S., Theory of Machines, Southward.CHAND
^ Schunck, Richard, "Minimizing gearbox noise inside and outside the box", Move System Design.
^ Vallance & Doughtie 1964, p. 281
^ ^a ^b Helical gears, archived from the original on 26 June 2009, retrieved 15 June 2009.
^ McGraw-Hill 2007, p. 742.
^ Canfield, Stephen (1997), "Gear Types", Dynamics of Machinery, Tennessee Tech Academy, Department of Mechanical Engineering, ME 362 lecture notes, archived from the original on 29 August 2008.
^ Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, p. 287, ISBN978-0-8284-1087-8.
^ ^a ^b McGraw-Hill 2007, p. 743.
^ Vallance & Doughtie 1964, p. 287.
^ Vallance & Doughtie 1964, pp. 280, 296.
^ Vallance & Doughtie 1964, p. 290.
^ McGraw-Hill 2007, p. 744
^ Kravchenko A.I., Bovda A.Thousand. Gear with magnetic couple. Pat. of Ukraine N. 56700 – Bul. N. ii, 2011 – F16H 49/00.
^ ISO/DIS 21771:2007 : "Gears – Cylindrical Anfractuous Gears and Gear Pairs – Concepts and Geometry", International Organization for Standardization, (2007)
^ Gunnar Dahlvig (1982), "Construction elements and machine construction", Konstruktionselement och maskinbyggnad (in Swedish), 7, ISBN978-9140115546
^ Hogan, C. Michael; Latshaw, Gary L. (21–23 May 1973). The Human relationship Between Highway Planning and Urban Noise. Proceedings of the ASCE, Urban Transportation Partitioning Specialty Conference. Chicago, Illinois: American Society of Civil Engineers, Urban Transportation Partitioning.
^ Smith, Zan (2000), "Plastic gears are more reliable when engineers business relationship for material backdrop and manufacturing processes during blueprint.", Motility System Design.
^ ^a ^b "W. K. Berg Gear Reference Guide" (PDF). Archived from the original (PDF) on 21 April 2015.
^ Oberg, East.; Jones, F. D.; Horton, H. 50.; Ryffell, H. H. (2000), Mechanism'southward Handbook (26th ed.), Industrial Press, p. 2649, ISBN978-0-8311-2666-vii.
^ "Elements of metric gear technology" (PDF).
^ Fred Eberle (Baronial 2014). "Materials Matter". Gear Solutions: 22.
^ Siegel, Daniel M. (1991). Innovation in Maxwell'southward Electromagnetic Theory: Molecular Vortices, Displacement Current, and Light. University of Chicago Press. ISBN978-0521353656.
^ MacKinnon, Angus (2002). "Breakthrough Gears: A Elementary Mechanical Organization in the Quantum Regime". Nanotechnology. xiii (5): 678–681. arXiv:cond-mat/0205647. Bibcode:2002Nanot..13..678M. doi:ten.1088/0957-4484/13/5/328. S2CID 14994774.
^ Sanduk, Thou. I. (2007). "Does the 3 Moving ridge Hypothesis Imply Hidden Structure?" (PDF). Apeiron. 14 (ii): 113–125. Bibcode:2007Apei...14..113S.
^ Sander, One thousand. (1957), "Bau und Funktion des Sprungapparates von Pyrilla perpusilla WALKER (Homoptera - Fulgoridae)", Zool. Jb. Jena (Anat.) (in German language), 75: 383–388
^ ^a ^b Burrows, Malcolm; Sutton, Gregory (13 September 2013). "Interacting Gears Synchronize Propulsive Leg Movements in a Jumping Insect". Science. 341 (6151): 1254–1256. Bibcode:2013Sci...341.1254B. doi:x.1126/science.1240284. hdl:1983/69cf1502-217a-4dca-a0d3-f8b247794e92. PMID 24031019. S2CID 24640726.
^ Herkewitz, William (12 September 2013), "The Commencement Gear Discovered in Nature", Popular Mechanics
^ Lee, Jane J. (12 September 2013), "Insects Use Gears in Hind Legs to Spring", National Geographic
^ Stromberg, Joseph (12 September 2013), "This Insect Has The Only Mechanical Gears E'er Constitute in Nature", Smithsonian Magazine , retrieved 18 Nov 2020
^ ^a ^b Robertson, Adi (12 September 2013). "The first-ever naturally occurring gears are constitute on an insect'due south legs". The Verge . Retrieved 14 September 2013.
^ Functioning 'mechanical gears' seen in nature for the beginning time, PHYS.ORG, Cambridge University

Bibliography

McGraw-Hill (2007), McGraw-Hill Encyclopedia of Science and Technology (10th ed.), McGraw-Hill Professional, ISBN978-0-07-144143-eight.
Norton, Robert Fifty. (2004), Design of Machinery (tertiary ed.), McGraw-Colina Professional, ISBN978-0-07-121496-4.
Vallance, Alex; Doughtie, Venton Levy (1964), Design of machine members (4th ed.), McGraw-Colina.
Industrial Press (2012), Machinery's Handbook (29th ed.), ISBN 978-0-8311-2900-2
Engineers Border, Gear Design and Engineering Data.

External links [edit]

Wikimedia Commons has media related to Cog wheels.

Geararium. Museum of gears and toothed wheels - antique and vintage gears, sprockets, ratchets and other gear-related objects.
Kinematic Models for Design Digital Library (KMODDL) - movies and photos of hundreds of working models at Cornell University
Brusk historical account on the application of analytical geometry to the form of gear teeth
Mathematical Tutorial for Gearing (Relating to Robotics)
American Gear Manufacturers Clan
Gear Technology, the Journal of Gear Manufacturing

gagnewishoune.blogspot.com

Source: https://en.wikipedia.org/wiki/Gear